| id_answer | r_it | P | n |
|---|---|---|---|
| N_from_df | 0.20 | 0.89 | 329 |
| alpha | 0.76 | 0.84 | 329 |
| beta | 0.81 | 0.81 | 329 |
| d | 0.22 | 0.63 | 329 |
| one_minus_alpha | 0.76 | 0.84 | 329 |
| power | 0.80 | 0.82 | 329 |
Bei dieser Aufgabe geht es um das visuelle Verständis eines Signifkanztests, eingebettet in einen Poweranalyse-Kontext. Die Daten sind fiktiv, da Populationswerte dargestellt werden.
Eine Zufallsvariante der Aufgabe sieht wie folgt aus (Achtung, die Aufgabe ist sehr lang durch die Abbildung):
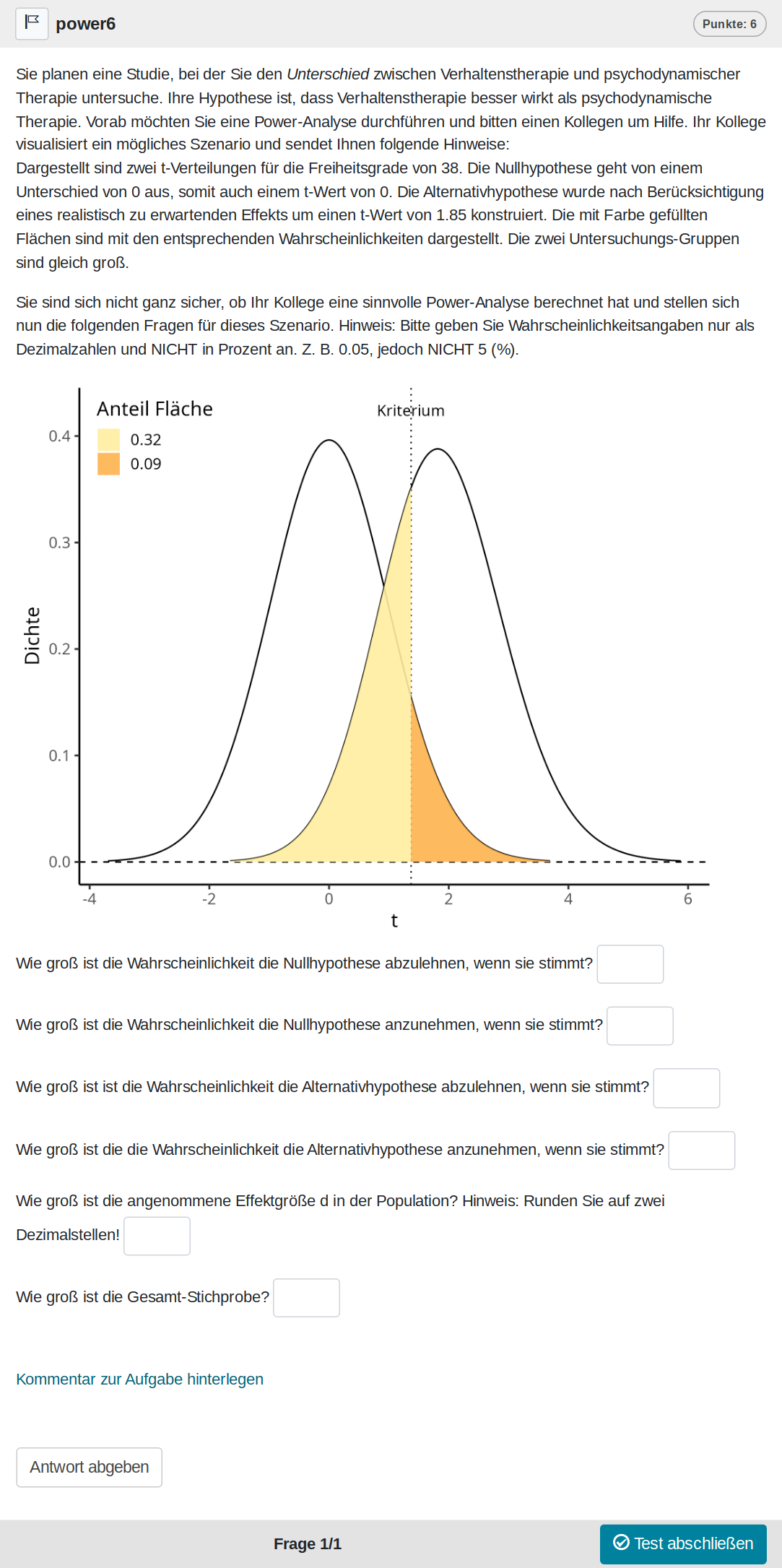
Und kann auf Opal auch direkt ausprobiert werden: Link
Für diese Aufgabe werden alle Lösungen im Feedback angezeigt. Bei Bedarf können weitere Details mit Studierenden in Übungen besprochen werden.
Die Aufgabe ist natürlich auch Bestandteil des Übungskurses: https://bildungsportal.sachsen.de/opal/auth/RepositoryEntry/38156107780/CourseNode/1691461670202015008
In diesem Fall ohne Modifikationen.
Validierung
Die Aufgabe ist noch nicht so lange in unserem Kanon, daher haben wir im Übungskurs nur einige Daten sammeln können. In einer Klausur kam die Aufgabe bisher nur ein Mal zum Einsatz. Zunächst die Übungsaufgaben (r_it ist die Trennschärfe, P die Itemschwierigkeit):
Die Bearbeitung der Aufgabe liegt bei 186s.
Deutlich wird hier, dass es zwei Gruppen von Fragen gibt. Das visuelle Verständnis des Signifikanztests (alpha, beta, power, one_minus_alpha) und die Berechnung der Effektgröße/Stichprobengröße (N_from_df, d). Das visuelle Verständnis dominiert die Aufgabe; dort besteht auch eine klare Abhängigkeit. Hingegen ist die Berechnung der Effektgröße/Stichprobengröße nicht prädiktiv für die Gesamtaufgabe. Hier kommen offensichtlich verschiedene Skills zum Einsatz. Die Berechnungen haben auch extremere Lösungsraten.
Für die Beurteilung der Aufgabe, ist eine Klausur natürlich aussagekräftiger:
| year | GROUP | r_it | P | dur | n |
|---|---|---|---|---|---|
| 2024 | 1 | 0.76 | 0.85 | 466.71 | 102 |
Die Trennschärfe ist ausgezeichnet, bisher die höchste, die wir je erreicht haben. Die Lösungsrate ist in einem guten Bereich. Die Aufgabe funktioniert also ziemlich gut. Schauen wir uns noch die Analyse auf Item-Ebene für die Klausur an:
| id_answer | r_it | P | n |
|---|---|---|---|
| N_from_df | 0.60 | 0.89 | 102 |
| alpha | 0.82 | 0.88 | 102 |
| beta | 0.73 | 0.87 | 102 |
| d | 0.45 | 0.66 | 102 |
| one_minus_alpha | 0.81 | 0.91 | 102 |
| power | 0.78 | 0.90 | 102 |
Hier sehen wir, dass alle Items prädiktiv für das Klausurergebnis sind. Am schwächsten schneidet die Berechnung der Effektgröße d ab, was auch das schwerste Item ist.
Aufgabe in R nutzen
Da sich die Hypothesen bei der Aufgabe zufällig ändern, kann es sinnvoll sein nur eine Version in einer Prüfung zu verwenden. Zur Illustration erstellen wir hier trotzdem 20 Versionen der Aufgabe:
library(methodenlehre)
aufgaben <- power(1:20)Diese könnten jetzt z. B. in eine Sektion gepackt werden, aus der man eine Variante zufällig zieht:
sektion <- section(aufgaben, selection = 1)Und der finale Test:
test <- test(identifier = "power", content = sektion)Weitere Details zur Aufgabenerzeugung kann man entsprechend im methodenlehre-Paket nachlesen.
QTI zum Download
Den Test, den wir oben erzeugt haben, können wir nun auch als QTI-Datei schreiben:
createQtiTest(test, ".", verification = TRUE, zip_only = T)[1] "./power.zip"Über verification wissen wir, dass es eine valide QTI-Datei ist. Und mit zip_only bekommen wir nur die gezippte Datei.
Diese Datei kann man jetzt in Learning-Management-Systeme, die QTI 2.1 unterstützen, importieren. Unter Opal wäre es dann auch möglich diesen Test in andere Tests zu inkludieren. Beispielsweise wenn man als Dozent schon eine Klausur erstellt hat und diese um unsere Aufgabe erweitern möchte.